一、写在前面
本题关于快慢指针的解法,网上有很多分享文章,很感谢这些作者,帮我解答了最初的疑惑。
但当自己想系统了解该算法时,却发现大部分文章存在两点不足:
数学证明不完整,或者过于复杂;关于时间复杂度的计算,没有详细说明。针对这两个问题,本文尽可能用简单的方式,叙述清楚,希望大家有所收获。
二、问题回顾及算法基本思想
问题:
若链表存在环,请找到入环点。
快慢指针算法思想:
定义快慢指针fast和slow,起始均位于链表头部。规定fast每次后移2步,slow后移1步;若fast遇到null节点,则表示链表无环,结束;若链中有环,fast和slow一定会再次相遇;当fast和slow相遇时,额外创建指针ptr,并指向链表头部,且每次后移1步,最终slow和ptr会在入环点相遇。三、疑问
为什么fast和slow一定会相遇?fast和slow相遇时,slow指针是否绕环超过一圈?为什么ptr和slow相遇的节点一定是入环点?为什么fast指针每次移动2步,能不能移动3、4、5...步?四、问题解答
PS:问题1、2、3的条件都是slow=1,fast=2。问题1:为什么fast和slow一定会相遇?
我们知道,两人绕操场跑圈,只要一直跑,快的肯定会追上慢的,即再次相遇。
但本题略有不同,我们可以把操场想成一个个格子组成的链表环,slow每次跳一格,fast每次跳两格,只有两人站在同一个格子上,才算相遇。如果是跳跃式的穿过,那是不算相遇的。
在此要求下,还能保证一定相遇吗,答案是肯定的。
我们来看slow和fast之间的距离,有以下几种情况:
相距1格,下次相遇。相距2格,下一次移动,变为相距1格。其它时刻,每次环内移动,距离缩短1,直至相距2格。通过分析可知,快慢指针一定会相遇。
问题2:fast和slow相遇时,slow指针是否绕环超过一圈?
我们先假设没有环外部分,整个链表就是一个环,slow和fast从环中同一点出发,fast的速度是slow的两倍。当slow绕环一圈,回到起点时,fast刚好跑完两圈,两者相遇。
当存在环外部分时,slow到达入环点时,fast指针已进入环内,相当于提前追赶了一段时间,将提前达到【相差一个格子】的状态。
因此,当slow=1,fast=2时,无论是否存在环外部分,相遇时,slow不可能绕环超过1圈。
问题3:为什么ptr和slow相遇的节点一定是入环点?
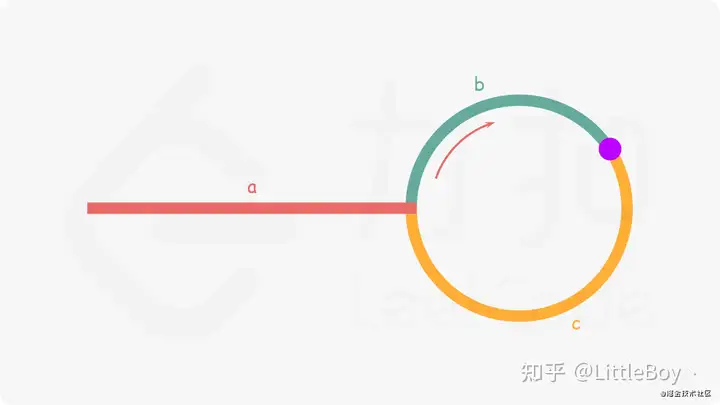
如图所示,假设环外部分长度为a,slow指针进入环后,又走了b的距离与fast相遇。此时,fast指针已经走完了环的n圈,因此它走过的总距离为: a+n(b+c)+b=a+(n+1)b+nc
任意时刻,fast指针走过的距离都为slow指针的2倍,而且由问题2的解答,我们已经知道,slow指针是不可能绕环超过一圈的,即相遇时,slow走的距离为a+b。因此得出关系式:
a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)
a=c+(n−1)(b+c)这个等量关系特别重要,其中c表示slow与fast指针相遇位置到入环点的距离,而(n−1)(b+c)则是 n-1圈的环长。
因此,只需要再添加一个指针指向头结点,当它走完环外距离a的时候,则会与在绕圈等它的slow相遇。而相遇点恰好是入环点。
问题4:为什么fast指针每次移动2步,能不能移动3、4、5...步?
设环外长度为w,环长度为s。取一特殊值j,保证j>w且是s整数倍的最小值。将slow走了j步后的位置记为X(j),则fast走了kj步,记为X(kj),其中k为fast与slow的速度比值。
因为j>w,所以slow和fast都在环内,而且X(kj)可以看做从X(j)出发,走了(k-1)*j步,因为j是环长的整数倍,所以又回到了X(j),两者相遇。
从上面的分析可知,无论fast取任何值,两者都会相遇。即使比值K是小数2.3(如slow=10,fast=23),也只需要j乘以10,就证明了这个问题。
我们之所以取fast=2,是因为快指针的时间复杂度为O(n*fast),可以保证算法效率最高。
五、复杂度分析
时间复杂度:O(N),N为链表节点数量,通过问题2、问题3的解答,slow与fast相遇时,slow不会绕环超过一周;寻找入环点时,也只走了环外距离a。因此,总的执行时间为:O(N)+O(N)=O(N)O(N)+O(N)=O(N)
空间复杂度:O(1)。因为只使用了slow、fast、ptr三个指针。六、代码
七、写在最后
有补充或者疑问的同学,欢迎评论区留言。
如果有所收获,大家也可以点点关注。感谢!
 sdf
sdf